Прикладная математика — область математики, рассматривающая применение математического знания в других сферах деятельности. Архимед был практик, Лейбницу нравилось знать причины. Чистая математика – теория. Что есть критерий истины? Практика. Теория практична или нет? Кирхгоф сказал "Нет ничего практичнее хорошей теории".

Галилей считает, что всё может быть описано на языке математики – на том, что сейчас мы называем математическими моделями.

Некоторые математики гордились тем, что они не запачкались приложениями. Например, Харди гордился тем, что его работы не нашли приложения.

Где кончается прикладная математика и начинается теория, трудно сказать. Например, кто прикладники: Ньютон, Архимед. Архимед призывал видеть за математическими результатами нематематические следствия. Рассказал Гиерну про свойства параболических зеркал, ссылался на свойства параболы. "Вероятно, когда ты узнал доказательство, ты радовался ему, некоторые построили следствия, я лишь пошёл ещё дальше и нашёл нематематические приложения".

Как строятся математические модели? Он должны соответствовать описываемому явлению и должны быть описаны математически. Возможно ли такое? В математике очень часто приходится прибегать к приближениям. Математические модели можно применять в естественных науках (физика, химия, биология, социология, экономика и т.д.).

Академиком А. Н. Колмогоровым предложена такая структура истории математики:

• Период зарождения математики, на протяжении которого был накоплен достаточно большой фактический материал;

• Период элементарной математики, начинающийся в VI—V веках до н. э. и завершающийся в конце XVI века («Запас понятий, с которыми имела дело математика до начала XVII века, составляет и до настоящего времени основу „элементарной математики“, преподаваемой в начальной и средней школе»);

• Период математики переменных величин, охватывающий XVII—XVIII века, «который можно условно назвать также периодом „высшей математики“»;

• Период современной математики — математики XIX—XX века, в ходе которого математикам пришлось «отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм».

С середины 20 столетия, по-видимому, есть некий рубеж, хотя бы появление компьютеров. Поскольку многие новые разделы математики появились именно с появлением вычислительной техники. Кроме того, появилась возможность решать то, что нельзя было решать ранее.

Александров Александр Данилович. Выдающийся геометр ленинградской школы, изучал геометрические свойства фигур, породившие, например, нерегулярные поверхности. Ему принесли известность работы по теории римановых пространств, «геометрия Александрова». Был спортсменом, альпинистом, лыжником.

Александров Павел Сергеевич был лектором на мехмате. Основатель всей современной топологической школы, родился в 1876 году, почётный представитель математического общества, почётный член большого количества иностранных университетов и академий, его ученики – Понтрягин, Тихонов.

Бернштейн Сергей Натанович. Работал в Харькове, Ленинграде, Москве. Работал в области теории вероятностей. Решал граничные задачи для уравнений эллиптического типа, продолжил исследование теорий Чебышёва, Маркова по приближенным многочленам. Полиномы Бернштейна используются при построении кривых Безье.

Боголюбов Николай Николаевич. В 16 лет стал аспирантом Академии Наук. Был директором института ядерных исследований. У него исследования по нелинейной механике, обосновывающие теорию сверхтекучести и сверхпроводимости.

Виноградов Иван Матвеевич. Возглавлял институт Стеклова 51 год. Специалист в теории чисел, тригонометрическим суммам, много приложил для создания учебников для школ и вузов.

Глушков Виктор Михайлович. Начинал с абстрактной математики, с абстрактной топологии. Результаты в области цифровых автоматов, автоматизации проектирования.

Ершов Андрей Петрович. Первый академик в области программирования. Родоначальник автоматизации программирования, первая программирующая программа. Ведущий теоретик в области программирования. Первый разработал теорию компиляции, интерпретации. Был назначен руководителем создания учебника по информатике. Рецензировал учебник наш лектор. Это был образец того, как не надо писать учебники.

Лаврентьев Михаил Алексеевич. Организовывал сибирское отделение АН. Специалист в области ТФКП.

Келдыш Мстислав Всеволодович. Уникальный человек. Президент АН СССР. Был и организатор и учёный. Чем он занимался в математике: вычислительная математика, теория колебаний, теория приближений, занимался проблемами вычислительно-машинной математики. Отец космической математики.

Канторович Леонид Витальевич. Лауреат Нобелевской премии в области экономики за вклад в теорию оптимального распределения ресурсов.

Андрей Николаевич Колмогоров. Заведовал отделением математики на мехмате, был деканом мехмата. Разработал аксиоматику теории вероятности. Решил вместе с Арнольдом 13 проблему Гильберта. Родоначальник матем. статистики. публиковал серьёзные работы по тригонометрическим рядам, теории множеств., функциональному анализу. Колмогоров первым начал применение математики в лингвистике, биологии, в области конструктивной логики, топологии, механики, основополагающие результаты в теории вероятности, теории турбулентности, теории сложности алгоритмов. Исследовал качества массовой продукции (теория массового обслуживания), теория информации, результаты по теории стрельбы, математические методы в биологии, занимался вопросами школьного и вузовского образования.

Лев Семёнович Понтрягин. В топологии открыл общий закон двойственности и в связи с этим построил теорию характеров непрерывных групп; получил ряд результатов в теории гомотопий (классы Понтрягина). В теории колебаний главные результаты относятся к асимптотике релаксационных колебаний. В теории управления — создатель математической теории оптимальных процессов, в основе которой лежит т. н. принцип максимума Понтрягина (см. Оптимальное управление); имеет фундаментальные результаты по дифференциальным играм. Работы школы Понтрягина оказали большое влияние на развитие теории управления и вариационного исчисления во всём мире.  Он возглавлял кафедру ОУ. В 11 лет потерял зрение и вырос в одного из ведущих математиков мира. Лектору повезло слушать его лекции по дифференциальным уравнениям. Один из основоположником топологии.

А. Н. Тихонов. Первые работы Андрея Николаевича, сделанные в студенческие годы, посвящены топологии и функциональному анализу. В частности Тихоновым в 1926 году было введено понятие произведения топологических пространств — так называемое «тихоновское произведение», доказаны теоремы о бикомпактности произведения бикомпактных пространств и о существовании неподвижной точки при непрерывных отображениях в топологических пространствах. Фундаментальные результаты были получены им в области математической физики, теоретической геофизики, моделирования физико-химических процессов. А. Н. Тихоновым доказаны теоремы единственности для уравнения теплопроводности, изучены функциональные уравнения типа Вольтерра (1938).

В 1948 г. по распоряжению правительства А. Н. Тихонов организовал Вычислительную Лабораторию для расчёта процесса взрыва атомной бомбы. Он также выполнил фундаментальные исследования по разработке теории и методике применения электромагнитных полей для изучения внутреннего строения земной коры (1950).

А. Н. Тихонов — основоположник крупного направления в асимптотическом анализе — теории дифференциальных уравнений с малым параметром при старшей производной.

Под руководством Тихонова созданы алгоритмы решения многих прикладных задач. В 1956—1963 годах совместно с Александром Андреевичем Самарским развита теория однородных разностных схем.

Работа над проблемами поиска полезных ископаемых привела А. Н. Тихонова к концепции обратных и некорректных задач, к разработке методов регуляризации, тем самым к созданию крупного научного направления, получившего мировое признание. Введённое Тихоновым понятие регуляризации позволило разработать методы решения некорректных задач. Это научное направление он развивал на протяжении всей жизни.

Изучал температуры планетных тел, распределение температур в земной коре.

Занимался проблемами регуляризации, позволяющей решать некорректные задачи. За работы в этой области он удостоен звания героя социалистического труда, получил ленинскую премию. Человек разносторонний. Возглавил в 1960 году кафедру ВМ мехмата и одновременно возглавлял кафедру математики на физфаке и был директором института прикладной математики имени Келдыша.

Сергей Львович Соболев. 28 - член-корреспондент АН СССР, 32 — академик. Лектор просто вспомнит свое впечатление о заседании кафедры ВМ мехмата. Каждый, кто хотел защищать кандидатскую/докторскую, считал за честь доложиться на семинаре Соболева. Если Соболев в конце давал резюме, то всё становилось ясно. С. Л. возглавлял сибирское отделение АН, уехал в Новосибирк и тогда А. Н. его заменил.

Древние цивилизации образовывались вдоль крупных рек. Нил --- наиболее благополучная из таких рек. Поскольку, в отличии от других, у нее почти не менялось русло и орошение не было таким сложным. Знания о Египетской математике почерпнуты из двух папирусов, объясняющих решения по 86 и 25 прикладных задач.

Использовалась десятичная иероглифическая система счисления. Каждая десятичная единица более высокого разряда обозначалась своим иероглифом, очень похожа на римскую систему счисления. На этой системе египтянами построена довольно сложная арифметика. Умножение здесь сводится к повторным сложениям.

Арифметика: например, знали 10х12=24+96=120.

Использовали дроби вида 1/n. Была таблица для представления дробей вида 2/n, как сумму таких дробей. Были особые дроби 2/3 и 3/4. Как они записывали сумму дробей: 1/2 1/5 1/7

Считали площадь треугольника (половина произведения основания на высоту), прямоугольника, трапеции, круга. Площадь круга --- (8/9 d)^2, для Пи это неплохое значение.

Умели вычислять объём цилиндра, объём усечённого конуса, параллелепипеда.

Есть задачи на сумму геометрической прогрессии (в 7 домах 7 комнат, в них по 7 кошек).

Задачи на пропорциональное деление.

Математика носила прикладной, а не алгоритмический характер.

Ещё одно достижение --- ритуальные сооружения, пирамиды.

Климат там был очень жаркий, засушливый, жизнь зависела от орошения, Тигр и Евфрат меняли русло. Как результат более тяжёлых условий, уровень вавилонян был выше. Знания об их математике почерпнуты из сохранившихся глиняных табличек. До нас дошло примерно 200 дощечек с таблицами без текста и 50 табличек с математическими текстами.

Вавилоняне имели более прогрессивную позиционную 60-ричную систему счисления. Такая система имеет огромное преимущество при вычислениях по сравнению с римскими цифрами. Однако эта система не имела знака для нуля, что приводило к некоторой неопределенности, и точное истолкование записи надо было извлекать из контекста. Современное деление часа на 60 минут и 3600 секунд восходит к Вавилону. Это же относится к делению окружности на 360⁰, градуса на 60 минут, минуты на 60 секунд. Что касается авторства позиционности системы, то здесь не все ясно. Возможно это изобретение Индии, где десятичная позиционная система с нулем появилась около 500 года до н.э.

В Вавилоне владели техникой решения квадратных уравнений, тогда как египтянам были известны лишь линейные. Решали также задачи, сводящиеся к кубическим и биквадратным уравнениям. Такие задачи они формулировали только для определенных числовых значений коэффициентов. Ван дер Варден в книге “Пробуждающаяся наука” указывает, что вавилоняне умели решать следующие 10 видов уравнений и систем:

Уравнения

,

Системы

,

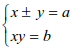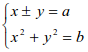
Кроме того они умели находить сумму арифметической прогрессии и суммы других видов, например,

Геометрические знания были выше египетских, уже встречаются некоторые тригонометрические соотношения. Площадь круга вычислялась по формуле S = , где c - длина окружности; отсюда p = 3. Есть основания полагать, что в Вавилоне была известна теорема Пифагора, поскольку у них есть таблица пифагоровых чисел. Но возможно саму Теорему Пифагора в чистом виде не знали. Умели вычислять зачатки выч. углов и тригонометрических соотношений.

Встречались следующие экономические задачи: через какое время удвоится сумма, выданная под 20 процентов годовых.

Древние греки создали основы того, что сейчас называется элементарная математика. Что этому способствовало? Прежде всего, переход от бронзы к железу, развитие ремёсел, производства, потом появились деньги, что в значительной степени способствовало торговле, обмену. Не последнюю роль играл более удобный алфавит. Развитие алфавита --- возможность перемещения, обмена.

Фалес Милетский (624---547 год до н.э). Вообще говоря, это был философ. Считал, что главное --- вода. Предсказал затмение, вычислял высоту пирамиды по тени, мог вычислить расстояние до корабля от берега. Что самое главное: он формулировал математические утверждения и их доказывал. Вот в чём принципиальное отличие математики Древней Греции --- они отвечали не только на вопрос как, но и почему. Формализованные им факты:

• Диаметр делит круг пополам

• Вертикальные углы равны

• В равнобедренном треугольнике углы равны

• Теорема Фалеса

В математике этого периода практические задачи, связанные с вычислениями, геометрическими измерениями и построениями, продолжали играть большую роль. Эти задачи постепенно выделились в отдельную область математики, названную логистикой. Она включала операции с целыми числами и дробями, решение задач, сводящихся к уравнениям 1-й и 2-й степени, практические задачи архитектуры, земледелия и т.п.

Пифагор искал основу всего сущего, и он считал таковой основой число. Не только чётные и нечётные, но и совершенные, дружественные (сумма делителей одного равна другому и наоборот, напр. 220 и 284). Пифагор обожествлял эти понятия и представления. Какие ещё были числа: треугольные, квадратные. Пифагорийцы не признавали прикладного характера математики. Будучи аристократами они считали, что решение практических задач - удел лишь низших сословий.

Пифагорийцами была построена значительная часть планиметрии прямолинейных фигур, доказана теорема Пифагора (она получила имя основателя греческой школы, хотя была известна значительно раньше в Вавилоне). Был найден способ отыскания целых пифагоровых чисел, удовлетворяющих соотношению : для нечетных n они имеют вид

.

Для четных n пифагоровы числа были получены позже в Академии знаменитого греческого философа Платона (427 - 347 г до н.э.) и равны

Из арифметики была выделена в отдельную область теория чисел - все, что относится к общим свойствам операций с натуральными числами. Целые числа представлялись основополагающими универсальными объектами, к операциям с которыми должны сводиться и все математические построения, и вообще все многообразие явлений действительности. Из этого принципа следовало, что отношения между любыми количествами должны быть отношениями целых чисел (т.е. рациональными числами).

Этому обожествлению целых чисел был нанесен сокрушительный удар самими же пифагорийцами. Оказалось, что отношение диагонали квадрата к его стороне ( равное ) не является рациональным числом, т.е. отношением целых чисел. Этот факт был доказан путем сведения к противоречию. Действительно, пусть где p и q - взаимно простые. Тогда и p - четное, а, значит, q - нечетное. Но из того, что следует , т.е. , а следовательно и q четные. Это был, по сути, первый кризис в математике. В то время еще не было предпосылок разрешить его, расширив понятие числа вводом иррациональностей. Осознав, что совокупность геометрических величин более полна, чем множество рациональных чисел, греки создали исчисление в геометрической форме. Новое исчисление получило в литературе название геометрической алгебры.

Еще одна трудность связана с тем, что греки не знали отрицательных чисел. Они имели дело с отрицательными числами только в терминах алгебраических выражений для площадей квадратов и прямоугольников, например, . Отрицательные числа впервые использовались, по видимому, китайцами, однако окончательно вошли в математику после работ Кардано в 1545 году.

Геометрическая алгебра греков. Первичными элементами ее являются отрезки прямой. С ними определены все операции исчисления. Возникающие при этом геометрические построения осуществляются циркулем и линейкой без делений. В геометрической алгебре сложение это приставление отрезков, вычитание - отбрасывание от отрезка части, равной вычитаемому отрезку. Результатом умножения принимается прямоугольник со сторонами a и b, равными перемножаемым отрезкам. Произведение трех отрезков дает параллелепипед. Произведение большего числа отрезков, естественно, не рассматривается. Деление наиболее сложная операция и возможно только, если размерность делимого больше размерности делителя, x=ab/c. Геометрическими построениями можно интерпретировать алгебраические формулы.

Созданному греками геометрическому исчислению свойственны, помимо неудобства, и более существенные недостатки. Довольно скоро выяснилось, что существует класс задач, не поддающихся решению с помощью циркуля и линейки. К ним относятся три знаменитые задачи древности:

- задача о трисекции угла, т.е. разделение произвольного угла на три равных части;

- задача об удвоении куба, т.е. определение ребра куба, объем которого вдвое больше объема заданного куба;

- задача о квадратуре круга, т.е. нахождение такого квадрата, площадь которого была бы равна площади заданного круга.

Евклид (около 300 до н.э.). Жил и работал в Александрии. Там был построен научный центр. Созрела необходимость в системе математики. Со своими обоснованиями, со своей системой логических выводов и доказательств. Евклидовы начала не были первыми. Первые были Гиппократа Хиосского, но они до нас не дошли.

Способы изложения «Начал» чрезвычайно громоздкие. Ещё Пифагор говорил, что заниматься числами было уделом избранных. В “Началах” систематизированы и строго изложены результаты, полученные математикой к III веку до н.э., включающие три важнейших открытия математики древности: теорию отношений Евдокса, теорию иррациональных Теэтета и теорию пяти правильных тел.

Первая книга содержала определения, аксиомы и постулаты.

Определения:

• Точка --- то, что не имеет частей.

• Линия --- длина без ширины.

• Куб --- телесная фигура, заключенная между 6 равными квадратами.

Аксиомы:

• Совмещение равно между собой

• Часть меньше целого

Постулаты:

• От всякой точки до всякой точки можно провести прямую.

• Ограниченную прямую можно непрерывно продолжать по прямой.

• Из всякого центра всяким раствором может быть описан круг.

• Все прямые углы равны между собой.

• Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

На протяжении последующих 2 тысяч лет многим казалось, что 5ый постулат можно доказать.

В первой книге даются основные действия над геометрическими примитивами и доказательство теоремы Пифагора. Метод доказательства такой: формализуется доказательство или утверждение, делается чертёж, доказательство по чертежу, дополнительные построения, если необходимо, и так далее. Тот метод, который использовал Евклид, называется синтезом.

Вторая. Геометрическая алгебра. Способы операций с отрезками, площадями, объёмами.

Третья. Свойства вписанных и описанных углов.

Сын астронома Фидия, гениальный изобретатель. III в до н.э.

Закон Архимеда (о ванне)

Другая легенда рассказывает, что построенный Гиероном в подарок египетскому царю Птолемею тяжёлый многопалубный корабль «Сиракузия» никак не удавалось спустить на воду. Архимед соорудил систему блоков (полиспаст), с помощью которой он смог проделать эту работу одним движением руки. (Дайте точку опоры, и я переверну землю)

Осада Сиракуз римлянами в 212 году до н. э. в ходе Второй Пунической войны. А ведь в это время ему было уже 75 лет! Построенные Архимедом метательные машины забрасывали римские войска тяжёлыми камнями. Мощные краны захватывали железными крюками корабли, приподнимали их кверху, а затем бросали вниз, так что корабли переворачивались и тонули. Были проведены несколько экспериментов с целью проверить правдивость описания этого «сверхоружия древности». Построенная конструкция показала свою полную работоспособность. По легенде, во время осады римский флот был сожжён защитниками города, которые при помощи зеркал и отполированных до блеска щитов сфокусировали на них солнечные лучи по приказу Архимеда. Легенда была дважды опровергнута в телепередаче «Разрушители легенд». Существует мнение, что корабли поджигались метко брошенными зажигательными снарядами, а сфокусированные лучи служили лишь прицельной меткой для баллист. В эксперименте греческого учёного Иоанниса Саккаса (1973) удалось поджечь фанерную модель римского корабля с расстояния 50 м, используя 70 медных зеркал. Только вследствие измены Сиракузы были взяты римлянами осенью 212 году до н. э. При этом Архимед был убит.

Нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида , корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.

Идеи Архимеда легли впоследствии в основу интегрального исчисления (вычислял площади и объемы).

Архимед сумел установить, что сфера и конусы с общей вершиной, вписанные в цилиндр, соотносятся следующим образом: два конуса : сфера : цилиндр как 1:2:3. В сочинении Квадратура параболы Архимед доказал, что площадь сегмента параболы, отсекаемого от неё прямой, составляет 4/3 от площади вписанного в этот сегмент треугольника.

Лучшим своим достижением он считал определение поверхности и объёма шара — задача, которую до него никто решить не мог. Архимед просил выбить на своей могиле шар, вписанный в цилиндр.

Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру. В работе «Об измерении круга» Архимед дал своё знаменитое приближения для числа π: «архимедово число» - три и одна седьмая.

Математика Востока, в отличие от греческой, всегда носила более практичный характер. Соответственно наибольшее значение имели вычислительные и измерительные аспекты. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия и астрология, механика, оптика.

В IX веке жил Аль-Хорезми — сын зороастрийского жреца, прозванный за это аль-Маджуси (маг). Изучив индийские и греческие знания, он написал книгу «Об индийском счёте», способствовавший популяризации позиционной системы во всём Халифате, вплоть до Испании. Сам он использовал и десятичную, и шестидесятиричную системы. В XII веке эта книга переводится на латинский, от имени её автора происходит наше слово «алгоритм» (впервые в близком смысле использовано Лейбницем), поскольку там излагались арифметические действия, алгоритмы. И алгоритмы связаны потом достаточно долго только с 4 арифметическими действиями. Другое сочинение аль-Хорезми, «Краткая книга об исчислении аль-джабра и аль-мукабалы», оказало большое влияние на европейскую науку и породило ещё один современный термин «алгебра». Получил решения различных квадратных уравнений с положительными коэффициентами (достигается перебрасыванием в соответствующую часть для смены знака).

Учёные Ближнего Востока занимались вопросами решения задач плоской и сферической геометрии. Многие из них уже отделяли астрономию от тригонометрии.

Омар Хайям (1043--1123): поэт-математик. "Алгебра - наука об уравнениях". Пытался искать решения уравнений третьей степени в виде общих точек конических сечений. Делал попытки доказать пятый постулат Евклида. Пользовался он 10-ной и 60-ной системами счисления. Он решал уравнения 2 и 3 степени, причём решал путём поиска точек пересечения конических сечений. Искал приближённые решения уравнений третьей степени. Это вообще характерно для учёных Ближнего Востока — поиск приближенных решений итерационными методами.

Насиред-дин: построил первую систему плоской и сферической тригонометрии. Тоже пытался доказать пятый постулат.

Улугбек (1394--1449), правитель Самарканда. Много внимания уделял науке. Построил в Самарканде обсерваторию и медресе (университет). Составил таблицу синусов (точнее, хорд) с точностью до девятого знака и с шагом в одну минуту.

Аль-Каши (XIII в.). Итерационные решения уравнений 2 степени. Вычислил 17 знаков pi, построив правильный 3*2^28-угольник.

Аба́к — счётная доска, применявшаяся для арифметических вычислений приблизительно с IV века до н. э. в Древней Греции, Древнем Риме. Доска абака была разделена линиями на полосы, счёт осуществлялся с помощью размещённых на полосах камней или других подобных предметов.

Впервые появился, вероятно, в Древнем Вавилоне ок. 3 тыс. до н. э. Первоначально представлял собой доску, разграфлённую на полосы или со сделанными углублениями. Счётные марки (камешки, косточки) передвигались по линиям или углублениям. В 5 в. до н. э. в Египте вместо линий и углублений стали использовать палочки и проволоку с нанизанными камешками.

В Европе абак применялся до XVIII века. В Средние века сторонники производства арифметических вычислений исключительно при помощи абака — абацисты — в течение нескольких столетий вели ожесточённую борьбу с алгоритмиками — приверженцами возникших тогда методов алгоритмизации арифметических действий.

В России счёты (аналог абака) появились в XVI веке и применяются до сих пор, хотя в последнее время их использование ограничено широким распространением калькуляторов.

Ацтекские счёты возникли приблизительно в X веке и изготавливались из зёрен кукурузы, нанизанных на струны, установленные в деревянной раме.

В странах Востока распространены китайский аналог абака — суаньпань и японский — соробан.

Логарифмическая линейка была основным инструментом, который использовали инженеры, конструкторы, прорабы, у каждого из них в кармане была такая линеечка и они получали результаты быстрее чем мы на калькуляторе, причём они не только складывали, делили, умножали, вычитали корни, но и возводили в степени, вычисляли логарифмы, решали системы уравнений.

Важным усовершенствованием техники вычислений было изобретение логарифмов, которые позволили свести к сложению не только умножение и деление, но и такие громоздкие операции как возведение в степень и извлечение корня. Логарифмам предшествовала идея сравнения геометрической и арифметической прогрессий, также с целью сведения операций к более простым. Действительно, возьмем две последовательности

а) ..., q^-1, q⁰, q¹, q², ...

б) ..., -1, 0, 1, 2, ...

Умножению членов последовательности а) соответствует сложение соответствующих членов последовательности б). На современном математическом языке эти последовательности задают функцию или . Но в те времена еще не знали показательной и логарифмической функции; они были введены лишь в XVIII веке Эйлером. Очевидно, если , то

Первые логарифмические таблицы были составлены швейцарцем Бюрги. Он работал в пражской астрономической обсерватории вместе с Кеплером, помогая ему в наблюдениях и вычислениях. У Бюрги основание логарифмов . Над таблицами логарифмов Бюрги трудился 8 лет, с 1603 по 1611 годы. Он их долго не публиковал и сделал это только в 1620 году благодаря настойчивым просьбам Кеплера. Это стоило Бюрги приоритета в изобретении логарифмов.

Изобретателем логарифмов считается шотландский математик барон Непер, опубликовавший в 1614 году в Англии книгу “Описание удивительных таблиц логарифмов”. Неперу принадлежит и сам термин “логарифм”. Книга Непера содержала 8-значные таблицы логарифмов тригонометрических функций для значений аргумента от до через . Непер исходил из двух последовательностей, из которых одна возрастает в арифметической прогрессии, а другая убывает в геометрической, что соответствует формуле

или ,

т.е. неперовские логарифмы имеют основание 1/е.

Непер и английский математик Бригг пришли к идее десятичной системы логарифмов, основанной на последовательностях а), б) при q=10. После смерти Непера Бригг в 1624 году опубликовал книгу “Логарифмическая арифметика”, содержавшую десятичные “бригговы” логарифмы с четырнадцатью знаками для целых чисел от 1 до 20.000 и от 90.000 до 100.000. Пробел был заполнен в 1627 году, когда голландец Влакк издал 10-значные таблицы логарифмов целых чисел от 1 до 10. В 1620 году англичанин Спейдель разработал таблицы натуральных логарифмов.

Первые логарифмические линейки были сделаны проф. Гюнтером, потом были инструменты Отреда и Деламейна, потом была междоусобица по поводу первенства между ними. Сейчас считается, что изобретение принадлежит обоим, и что они пришли к нему независимо друг от друга. Оба использовали обычный и круглый варианты линеек. Отред прожил 85 лет, он был роялист, когда он узнал о реставрации королевской власти (приход Карла IV), скончался. Роберт Бесакер в 1654 г. придумал линейку, очень похожую на нынешнюю (т.е. ту, которая была 30 лет назад). Была ещё спиральная линейка. Дж. Уатт также усовершенствовал линейку в 1779, разработав удобное расположение логарифмических шкал для универсального использования. В России появилась линейка в 1837, тогда как первые разработки были в 1620. Ньютон пользовался линейкой для решения СЛАУ, количество линеек пропорционально количеству шкал. Прозрачная планочка с риской --- идея Ньютона.

Важным событием, повлиявшим на процесс возрождения науки в Европе, была организация, начиная с XI века, учебных заведений. Одна из первых школ была создана в X веке во Франции ученым монахом Гербертом, будущим римским папой Сильвестром II. В школе обучали в основном технике счета. Начиная с XII века в Европе возникают университеты, вначале в Италии (в Болонье и Салерно), затем в Оксфорде и Париже (1167г.), Кембридже (1209г.), Неаполе (1224г.) и других городах. Первые университеты способствовали распространению знаний среди населения. Изучаемые дисциплины включали в себя и математику.

Период XV, XVI веков, называемый Возрождением, характеризуется существенными сдвигами во всех областях общественной деятельности: промышленности, технике, науке и искусстве. Именно в этот период европейская математика превзошла, наконец, достижения ученых Греции и арабского мира. Это было сделано в области алгебры, когда было получено общее алгебраическое решение кубических уравнений, тогда как греческие и восточные ученые решали лишь частные численные уравнения 3-й степени. Первые результаты были получены профессором Болонского университета Ферро. Уравнения третьей степени можно свести к трем типам

где p, q - положительные числа. Ферро решил эти уравнения, но не публиковал результатов, приберегая их для научного диспута, которые были распространены в то время. К сожалению, он скончался, не успев воспользоваться ими. Независимо решение было получено в 1535 году венецианским математиком Тарталья. Для уравнения он поступает так. Делается подстановка что приводит к соотношению

или

.

Положив Тарталья приходит к системе

Дело сводится к решению квадратного уравнения, что дает

или корень . Тарталья долго не публиковал свое решение. Дело в том, что он столкнулся с трудностью, преодолеть которую не мог, с так называемым неприводимым случаем. Решая уравнение с помощью подстановки , он получил

.

При под корнем получается отрицательное число. А Тарталье было известно, что существует корень уравнения. Сейчас мы знаем, что в этом случае все три корня кубического уравнения вещественны и выражаются через комплексные величины. Отмеченный факт послужил толчком к исследованиям, которые привели к созданию теории комплексного числа.

Джероламо Кардано был очень богатым и неординарным человеком с необычной судьбой. Он был разносторонне талантлив. Занимался математикой, астрономией, философией, медициной. Был изобретательным инженером: предложил подвес, ставший прообразом карданного механизма. Увлекался астрологией и предсказал год своей смерти - 1576. В этот год он объявил голодовку и умер на 75-ом году жизни. Несмотря на жизненные невзгоды - он потерял сына, который был казнен, лишился своего огромного состояния - Кардано увлеченно занимался наукой.

Кардано готовил большой математический труд “Великое искусство или о правилах алгебры”. Ему очень хотелось включить туда результаты Тартальи по кубическим уравнениям. Он выманил у Тартальи секрет под клятвенное обещание не разглашать его. Однако опубликовал, хотя и со ссылкой на автора. Тарталья был возмущен, завязалась долгая и ожесточенная полемика. Трудно сказать, что нового внес сам Кардано в решение Тартальи, но для потомков осталась формула Кардано, а не Тартальи.

Кардано тоже не смог одолеть неприводимого случая. Некоторая ясность была внесена последним из больших болонских математиков Бомбелли. В своем труде “Алгебра” (1572) Бомбелли развил теорию комплексного числа. Он вводит правила действий над комплексными числами a+bi, опирающиеся на i²=-1. На примере уравнения x³=15x+4 он показал, что в неприводимом случае вещественный корень получается как сумма соотношение двух комплексных чисел a+bi и a-bi.

Возник вопрос: решить уравнения 4, 3 степени мы можем. Уравнения 4 степени сводятся к уравнениям 3 степени заменой переменных. А как решать уравнения более высоких степеней? Этот вопрос повис. Этот вопрос до 19 века провисел, пока его не удалось решить Абелю и Галуа. Они доказали, что общих формул нет.

В XVII веке берут начало большинство математических дисциплин, которые ныне составляют основу высшего математического образования: математический анализ (Ньютон, Лейбниц), аналитическая геометрия (Декарт, Ферма), проективная и дифференциальная геометрия (Паскаль, Гюйгенс, Кеплер), теория вероятностей (Якоб Бернули, Ферма).

Рене Декарт (1596 - 1650). Правовед по образованию, физик, математик, физиолог. Родился во французском городе Турени в семье, принадлежащей древнему дворянскому роду. Образование получил в иезуитском колледже. Некоторое время служил в армии. Из-за разногласий с церковью долгое время жил в Голландии, и за год до смерти переехал по приглашению шведской королевы в Стокгольм.

Целью деятельности Декарта была разработка общего математического подхода к изучению естествознания. В труде “Геометрия”, вышедшем в 1637 году, он осуществил свой подход, объединив алгебру и геометрию. Главная заслуга Декарта состоит в систематическом применении уже хорошо развитой алгебры к геометрии, что существенно расширило область ее применения и создало основу для формирования самостоятельной математической дисциплины - аналитической геометрии.

Впервые использовал понятие переменной величины. Большое значение для дальнейшего развития математики имело и окончательное освобождение Декартом от ограничений, связанных с размерностью величин, идущих еще от геометрической алгебры древних греков.

Система координат. Систему координат Декарт воспринимал в двояком виде. Первый вид может показаться не вполне стандартным, он похож на беговые дорожки, где отмечены расстояния. И первый вариант у него есть система привязок к некой траектории, второй же вариант мы называем декартовой системой координат. Декарт использовал только первую четверть. В его системе координат не было даже оси Y, только ось X. Пространственных координат еще не было.

Декарт считал допустимыми только те прямые, которые рисуются только циркулем и линейкой, шарнирным механизмом. Он классифицировал кривые, давая ранг кривой, определённым количеством звеньев шарнирного механизма, которым можно нарисовать кривую. Это была первая попытка классифицировать кривые. Остальные кривые были названы механическими. Позднее Лейбниц назвал их трансцендентными.

Не любя отрицательные числа, высказал предположение о том, что у уравнения n-й степени n корней. Высказал предположение, что количество положительных корней уравнения соответствует числу знакоперемен (минус чётное число).

Уравнения 3, 4 степени он решал тригонометрическими методами, используя метод, аналогичный методу вставки в трисекции угла.

У него появились удобные обозначения +, -, = и · ввёл Декарт. y^2 — тоже Декарт. Неизвестные начал называть x, y, z, известные — a, b, c.

Пьер Ферма родился в 1601 году на юге Франции в семье торговца. Окончил юридический факультет Тулизского университета и работал юристом в Тулузе до конца жизни. Ферма самостоятельно знакомился с математикой, творчески работал в этой области и получил значительные результаты в разных математических дисциплинах, которые были опубликованы лишь после его смерти. Результаты Ферма по аналитической геометрии изложены в небольшой работе “Введение в теорию плоских и пространственных мест”, опубликованной лишь в 1679 году. Здесь уже содержатся уравнения

,

для прямых линий и конических сечений относительно перпендикулярных осей. В отличие от Декарта он рассматривает и общие уравнения 2-го порядка и сводит их сдвигом и поворотом осей к каноническому виду. Пространственной координаты у Ферма еще не было, но он изучает пересечения поверхностей плоскостями.

Ферма и Паскаль считаются основателями теории вероятностей. В 1654 году они установили ряд основных положений теории вероятностей на примере азартных игр.

Изучая перевод работ Диафанта, Ферма сформулировал на полях этой книги ряд утверждений по теории чисел, которые известны как теоремы Ферма. Ферма их не доказывал, вернее нет сведений об этом. Великая Теорема Ферма: x^n+y^n=z^n не имеет решений в целых числах при n>2. Доказательство для n=3 было получено лишь Эйлером. Сформулировав эту теорему, Ферма добавляет: ”Я нашел поистине удивительное доказательство этого предложения, но поля книги слишком узки, чтобы его изложить”. Если Ферма и знал доказательство, то оно никогда не было опубликовано. Все попытки математиков доказать эту теорему оказывались неудачными.

Умел решать задачи на отыскание экстремумов, построение касательных. В наших обозначениях он получил условие экстремума и выражение для подкасательной

Появились зачатки аналитической геометрии. Раз есть система координат, раз есть уравнения, Ферма показал, что прямым соответствуют уравнения первой степени, коническим сечениям — второй, причём приводил к каноническому виду.

В XVII веке многие крупные ученые проводили исследования, относящиеся к анализу бесконечно малых: Кеплер, Галилей, Кавальери, Торричелли, Паскаль, Валлис, Ферма, Декарт, Барроу. Они подготовили основу, на которой в конце века Ньютон и Лейбниц создали, независимо друг от друга дифференциальное и интегральное исчисление. Смысл бесконечно малой еще не был ясен в то время. Под ней понимали неизменяющуюся величину, не равную нулю, но меньшую любой конечной величины (актуально бесконечно малая). К пониманию бесконечно малой как к переменной величине, которая в процессе своего изменения становится меньше любой конечной величины, математика придет значительно позже.

Кеплер для вычисления объемов тел пользуется алгоритмом оперирования с бесконечно малыми, следуя Архимеду, однако не заботясь особенно о строгости доказательств, свойственной Архимеду. Он исходит из того, что фигура или тело состоит из множества бесконечно малых частей. Так, круг состоит из бесконечно большого числа бесконечно малых секторов, которые можно считать равнобедренными треугольниками. Треугольники имеют одинаковую высоту - радиус круга, а сумма их оснований составляет окружность. Точно также шар состоит из бесконечного множества пирамид с общей вершиной в центре. Метод суммирования бесконечно малых Кеплер распространил на тела вращения. Например, в случае тора он проводит меридиональные плоскости. Образующиеся ломтики он заменяет цилиндриками с общим основанием и средней высотой. Сумма их объемов составляет объем тора и равна объему цилиндра с высотой равной длине окружности, описываемой центром круга. В своем труде Кеплер вычислил объемы 87 новых тел вращения.

Бонавентура Кавальери (1598-1647), родом из знатной итальянской семьи, возглавлял кафедру математики в Болонском университете, будучи одновременно настоятелем монастыря. Большую известность получил его метод неделимых, разработанный в трудах “Геометрия, изложенная новым способом неделимых непрерывного” и ”Шесть геометрических опытов”, вышедших в свет соответственно в 1635 и 1647 годах. Согласно этому методу фигуры состоят из параллельных отрезков прямых, а тела-из плоскостей. Это и есть неделимые, их бесконечно много и они не имеют толщины. Кавальери понимал логические трудности, возникающие при составлении площади из прямых, не имеющих ширины, а объема - из плоскостей, лишенных толщины. Кавальери сущность метода формулирует так: плоские фигуры (или тела) относятся как все неделимые, взятые вместе. Эта формулировка очень туманна. По-видимому, все же неделимые находятся на равных расстояниях друг от друга и вместо отрезков берутся прямоугольники малой площади.

Наиболее отчетливо понятие определенного интеграла выявляется у французского ученого Блеза Паскаля (1623-1662). Он был известным математиком, физиком и философом. Последние годы жизни провел в монастыре, не бросая, однако, занятий наукой и философией. В работе “Общий трактат о рулетте”, посвященной исследованию неалгебраической кривой циклоиды (рулетты), Паскаль при вычислении площади использует зависимую и независимую переменные и суммирует значения функции, умноженные на приращения независимой переменной. В этой же работе появляется “треугольник Паскаля” - прообраз дифференциального треугольника (dx,dy,ds) Лейбница.

Паскаль получил также значительные результаты в области проективной геометрии, теории вероятностей, теории чисел, алгебре. Разработал метод математической индукции.

В 9 лет начал читать математическую литературу, отец испугался и запретил ему. В 12 тайком от отца он доказал, что сумма углов треугольника равна сумме двух углов прямоугольника, стал посещать математический кружок. В 16 лет он доказал теорему из проективной геометрии (о конических сечениях), распечатал и расклеил по улицам Парижа.

В 1623 Вильгельм Шикард придумал Считающие часы Вильгельма Шикарда — первый механический калькулятор, умевший выполнять четыре арифметических действия. Считающими часами устройство было названо потому, что, как и в настоящих часах, работа механизма была основана на использовании звёздочек и шестерёнок. Практическое использование это изобретение нашло в руках друга Шикарда, философа и астронома Иоганна Кеплера. Сложение 6-разрядных чисел. Самая тяжёлая задача - перенос десятков. Поставили ещё одно однозубое колесо.

Блез Паскаль (1623--1662) родился в достаточно обеспеченной семье рантье Этьена Паскаля. В 1638 отец попал в немилость к Ришелье и вынужден был бежать в Испанию. Позже по просьбе младшей дочери Этьен был прощен и занял пост интенданта Руана. В шестнадцатилетнем возрасте Блез опубликовал первую работу по математике (на 53 строки математического труда, размножил в 50 экземплярах и расклеил по улицам Парижа). Это был трактат по проективной геометрии "Опыт о конических сечениях".

В 18 лет начал разрабатывать вычислительные машины (около 50 штук). Идеи очень напоминали Шиккардовские. Но он точно не мог их увидеть, потому что никто о той машине и её идеях, кроме самого Шиккарда и его друзей, не знал. Машина Паскаля умела складывать, вычитать (используя дополнительный код), умножать и делить (путем последовательных сложений или вычитаний) разноразрядные числа. Проблема была с переносом десяток. Было 10ти и одно-зубное колеса, но технически реализовать в 1642 это было трудно. Кроме колёс использовались цепи, конуса, цилиндры. Он нанимал лучших механиков Франции, и они не справлялись с задачей, он сам готовил детали. Использовались медь, латунь, слоновая кость. Машина заработала, модель была отправлена шведской королеве Кристине. Современники считали её слишком сложной. Физически пользоваться машиной было тяжело, изнашивались колёса, возникал люфт.

Лейбниц описал двоичную систему счисления, центральный ингредиент всех современных компьютеров. Однако вплоть до 1940-х, многие последующие разработки (включая машины Чарльза Бэббиджа и даже ЭНИАК 1945 г.) были основаны на более сложной в реализации десятичной системе, в том числе сам калькулятор Лейбница. В нем добавляется умножение и деление. Для умножения – метод многократного сложения.

Перро Клод (1613-88), французский архитектор, брат Шарля Перро. Среди изобретений Клода Перро – «машины для поднятия тяжестей», «маятниковые часы, приводимые в движение с помощью воды», «машина для увеличения эффекта огнестрельного оружия», «система рычагов для вращения зеркала телескопа» и многие другие. Под номером десять в «Сборнике» числится изобретение, объясняющее наш интерес к Клоду Перро,– это суммирующая машина, в которой взамен зубчатых колес используются зубчатые рейки (кремальеры). Его машину также называют рабдологический абак.

В середине прошлого века З.Я. Слонимский (1810-1904) предложил простое множительное устройство, основанное на доказанной им теореме. Это устройство позволяло получать произведения любого числа (разрядность которого не превышала разрядности устройства) на любое однозначное число. Другими словами, это было нечто вроде механической таблицы умножения любого числа на 2, 3, 4,..., 9. 

Демидовскую премию получил, потратил на усовершенствование машины (вычислительный снаряд). Допускала самопроверку. Усовершенствовал машину Уатта, квадруплексную связь на телеграфе, в минсвязи отказали за ненадобностью, через 30 лет это переизобрёл Томас Альва Эдисон. Через 100 лет (в 1949) в Днепропетровске выпускали машины Прогресс, основанные на идеях Слонимского.

Первый арифмометр Чебышева, строго говоря, не может быть отнесен к классу арифмометров (приборов для выполнения четырех арифметических действий). Это 10-разрядная суммирующая машина с непрерывной передачей десятков. В машине с непрерывной (дискретной) передачей колесо высшего разряда продвигается сразу на одно деление, в то время как колесо низшего разряда переходит с 9 на 0. При непрерывной передаче десятков соседнее колесо (а вместе с ним и все остальные) постепенно поворачивается на одно деление, пока колесо младшего разряда совершает один оборот. Чебышев достигает этого применением планетарной передачи.

Работа оператора при выполнении сложения на машине Чебышева была очень простой. С помощью десяти наборных колес поочередно вводились слагаемые, а результат считывался в окнах считки. На наборных колесах имеются специальные зубцы, с помощью которых поворачиваются колеса. В корпусе машины - прорези, в которых видны эти зубцы, а рядом с прорезями написаны цифры (0...9). При вычитании набирается уменьшаемое, а вычитаемое нужно набирать, вращая наборные колеса в обратную сторону. В целом машина приспособлена для сложения, и вычитание на ней неудобно.

Следующими этапами работы Чебышева явились постройка новой модели суммирующей машины и передача ее в 1878 г. в Парижский музей искусств и ремесел, а затем создание множительно-делительной приставки к суммирующей машине. Эта приставка также была передана в музей в Париже (1881 г.). Таким образом, арифмометр, хранящийся в этом музее, состоит из двух устройств: суммирующего и множительно-делительного. Суммирующее устройство отличается от хранящейся в Ленинграде суммирующей машины несколькими несущественными усовершенствованиями, а также большим удобством в работе.

Ряд новых идей был воплощен и во множительно-делительном устройстве. Главная и наиболее плодотворная из них состояла в автоматическом переводе каретки из разряда в разряд. Кареткой, т. е. подвижной частью арифмометра, служила сама приставка. Для выполнения умножения и деления она устанавливалась на суммирующей машине, образуя с ней единый прибор. При выполнении умножения нужно было только вращать рукоятку арифмометра. 

Исаак Ньютон (1642-1727) родился близ Кембриджа в семье землевладельца. Учился в Кембриджском университете у Барроу. В 1669 год, всего лишь через год после получения Ньютоном звания магистра, Барроу передал ему свою кафедру. В университете Ньютон работал до 1696 года, после чего поступил на службу в ведомство монетного двора вначале в качестве инспектора, а затем директора. В 1672 году он избирается членом Лондонского королевского общества, а с 1703 года становится его президентом. Ньютон пользовался в научных кругах исключительным авторитетом как автор фундаментального научного труда “Математические принципы натуральной философии”, вышедшей в свет в 1687 году.

Ньютон получил исключительной важности результаты в механике, физике, астрономии и математике. Он сформулировал три основные законы механики, установил фундаментальный закон всемирного тяготения, который гласит: две материальные точки притягиваются с силой, пропорциональной произведению их масс и обратно пропорционально квадрату расстояния между ними. Строго математически из закона тяготения вывел законы движения планет вокруг Солнца, установленные Кеплером опытным путем. Дал объяснение приливов, заложил основы теории движения Луны, решил задачу двух тел для сфер. В физике он получил основополагающие результаты о распространении световых волн, исследовал интерференцию и дифракцию, открыл дисперсию света и хроматическую аберрацию. Сконструировал телескоп.

К интегральному и дифференциальному исчислению Ньютон пришел при разработке математического аппарата механики, который учитывает движение и связанные с ним понятия скорости и ускорения. На Ньютона оказало влияние сочинение Валлиса “Арифметика бесконечных”. Изучая его, Ньютон обобщил понятие бинома и пришел к биномическому ряду, который расширил область применимости его теории дифференцирования.

Свой метод Ньютон назвал методом флюксий. Он был разработан в 1665, 1666 годах, а опубликован лишь в 1736 году уже после смерти Ньютона в трактате “Метод флюксий и бесконечных рядов”. Ньютон не спешил публиковать свои открытия. С большим опозданием вышла в свет и “Всеобщая арифметика”, содержащая важные результаты по алгебре.

Флюксиями Ньютон называл производные по времени и обозначал точками над переменными. Позднее Ньютон ввел вторую флюксию , т.е. флюксию от флюксии, и флюксии более высоких порядков. Флюэентами он называл первообразные. Если в соотношении, связывающем флюенты встречаются дроби или радикалы, Ньютон действует по правилам дифференцирования сложной функции. С помощью рядов он распространяет свою теорию на трансцендентные функции. Исчисление флюксий Ньютон применяет для нахождения наибольших и наименьших значений функций, построения касательной и кривой, определения кривизны кривой. Все эти задачи методом флюксий решаются без труда.

Вторая основная задача заключается в определении соотношения между флюентами по заданному соотношению между флюксиями. Это обратная задача - задача интегрирования дифференциального уравнения, в частности нахождение первообразной. В общем случае эта задача представляет больше трудности. Постепенно сформировалась самостоятельная математическая дисциплина - теория обыкновенных дифференциальных уравнений. Ньютон находил решение отдельных дифференциальных уравнений, как правило, с помощью бесконечных рядов. Задачу нахождения первообразной Ньютон трактует геометрически как задачу квадратуры кривой.

Теорема Ньютона-Лейбница

Если  непрерывна на отрезке  и  — ее любая первообразная на этом отрезке, то имеет место равенство

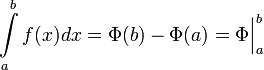
Используя это утверждение, Ньютон решает задачу определения кривой, площадь которой задается с помощью конечного уравнения. Он исходит из некоторого уравнения между x и z, находит уравнение между x и и отсюда определяет кривую. Он формулирует и решает с помощью подстановок и более сложную задачу определения кривой, площадь которой связана с площадью некоторой данной кривой конечным уравнением. С помощью таких приемов Ньютон получил большое число квадратур. Ньютон пытался обосновать теорию флюксий. В своем основном труде “Математические начала натуральной философии” он строит своеобразную теорию пределов, которая называется “Метод первых и последних отношений”. Пользоваться этой теорией было трудно; Ньютон, по видимому, не был ей удовлетворен. По крайней мере, в “Началах” нет никаких упоминаний о теории флюксий, хотя по утверждению самого Ньютона многие результаты, вошедшие в эту книгу, получены с помощью метода флюксий. Создавая теорию первых и последних отношений, Ньютон подошел к современному пониманию бесконечно малой. Он пишет: “Если в последующем для простоты речи я буду говорить о величинах весьма малых или исчезающих или зарождающихся, то не следует под этим разуметь количеств определенной величины, но надо их рассматривать как уменьшающиеся беспредельно”.

Одновременно с Лейбницем получил связь дифференцирования и интегрирования. Они дружили.

Готфрид Вильгельм Лейбниц (1646-1716) родился в Лейпциге в семье профессора университета. Учился в Лейпцигском и Йенском университетах. Многие годы находился на службе при дворе ганноверских герцогов. По делам службы посетил ряд европейских стран, где встречался с видными учеными. Был членом Лондонского королевского общества и Парижской академии наук. Основал Берлинскую академию и научный журнал в Лейпциге. Оказал влияние на развитие науки в России. Лейбниц был видным дипломатом, политиком, философом и ученым в области физики, права, литературы и языкознания и, конечно, крупнейшим математиком. Думал, что на основе математики можно составить всеобщий метод познания мира. В 18 лет написал докторскую по праву, но ему не дали степень. В 20 получил докторскую степень по праву. Говорил, что надо направить ученых мужей в Россию, составлял по этому поводу разные планы. Получил даже звание тайного советника от Петра I. Одну из своих ВМ отправлял в Россию, но она не дошла. Петр I тепло к нему относился и ценил его заслуги. В 1673 был принят в Лондонское королевское общество. В 1700 – член Парижской академии наук.

Идеи дифференциального исчисления изложены в маленькой журнальной заметке 1684 года “Новый метод для максимумов и минимумов, а также для касательных, для которого не являются препятствием дробные и иррациональные количества, и особый вид исчисления для этого”. Он мыслил в терминах характирестического треугольника (dx, dy, ds), ранее встречавшегося в работах Паскаля и Барроу. Дифференциал аргумента dx Лейбниц понимает как бесконечно малую разность. Дифференциал функции dy определяется из соотношения , где - подкасательная. В статье даны правила дифференцирования суммы, произведения, частного, степени. Получено условие dy=0 для экстремальных значений функции и d²y=0 для точек перегиба. Через два года вышла статья Лейбница “О глубокой геометрии”, в которой были даны правила интегрирования. Следуя Паскалю и Кавальери, он представлял интеграл как сумму “всех” ординат, которых бесконечно много. Он вводит для интеграла современный символ . Для трансцендентных функций использует ряды. Получает формулу многократного дифференцирования произведения функций, которая носит его имя. Символика и термины Лейбница (!!) оказались хорошо продуманными, удобными, и многие из них дошли до наших дней. Лейбниц ввел термины: дифференциал, дифференциальное и интегральное исчисление, дифференциальное уравнение, функция, координаты и др.

С появлением двух статей Лейбница о дифференцировании и интегрировании начался исключительно плодотворный период для математики. Начиная с 1687 года с Лейбницем стали активно сотрудничать братья Якоб и Иоганн Бернулли. До конца века они втроем разработали значительную часть современного интегрального и дифференциального исчисления. В 1696 году появился первый учебник по дифференциальному исчислению ученика Иоганна Бернулли маркиза Лопиталя “Анализ бесконечно малых”, как результат обработки лекций своего учителя. Здесь уже встречается известное правило Лопиталя раскрытия неопределенности типа 0/0. Это правило сообщил Лопиталю в одном из писем Бернулли.

Получил разложение в бесконечный ряд для числа Пи.

Установил связь между дифференцированием и интегрированием – не доказывал, но предполагал. udv = vdu – vu. Сформулировал некоторые правила дифференцирования. Дал приемы дифференцирования рациональных дробей.

Сходимость знакочередующегося ряда.

Правило Крамера.

В 1670 году принялся совершенствовать машину Паскаля. Он постоянно ее совершенствовал до 1704. Для механиков того периода было непросто ее реализовать. «Недостойно тратить часы на вычисления».

До XVIII века общий уровень культуры и науки в России был весьма низким. Первое высшее общеобразовательное учебное заведение было основано в Москве в 1687 году. Это была Славяно - греко - латинская академия, созданная для подготовки кадров для нужд государства и церкви и преподавателей школ. Поначалу математики в ней не было. Положение начало меняться в связи с проведением Петром I реформ, которые коснулись и вопросов образования, культуры и науки. В 1701 в Москве открылась школа навигационных и математических наук (в Сухаревой башне). Затем был создан еще ряд технических учебных заведений: артиллерийская школа, морская академия и др.

Петр I осознал необходимость образования в России. Посылал за границу обучаться, но никто не хотел ехать. Он отправлял насильно, но те люди терялись за рубежом и толк был незначительный. Тогда он привез преподавателей сюда. Начали писать учебники, открыта навигацкая школа в Сухаревской башне. Там обучали арифметике, геометрии, мореходным наукам, навигации и т.д. В 1715 году была открыта в Питере морская академия. В 1714 году – артиллерийская школа. Было кому читать лекции, но не было учеников. Надо было силой сгонять учащихся. Синод требовал, чтобы церковников освобождали, Посад – чтобы купцов. В 1716-22 годах цифирные школы (там преподавали военные) набрали 2000 человек, в 1727 году осталось 500. Выбыли посадские и духовные, кто-то не явился, кто-то выбыл по причине необучаемости. Первый русский учебник – «Арифметика» Магницкого в 1703, изложена в стихотворной форме. По ней учились многие поколения. Ломоносов знал ее наизусть (хотя может это миф). Магницкий был самоучкой, поглощал западную литературу, греческих, латинских авторов. В книге изложены задачи на баранов, овощи, прогрессии, проценты, квадратные уравнения. Даже у Евклида в его началах не было решений квадратных уравнений. А у Магницкого есть. Но он не хотел иметь дела с отрицательными коэффициентами.

Петербургская академия наук в 1725 году насчитывала 17 действительных членов и была сформирована целиком из иностранных ученых, в основном немецких. Первым русским членом академии стал М.В. Ломоносов (1745 г). Профессора ходили друг к другу на лекции из-за недобора. Гимназистов уже не стали набирать, вербовали детей солдат и т.п. Университет Академический Петербуржский был закрыт впоследствии княгиней Дашковой, потому что в общей сложности там училось 2 студента.

Леонард Эйлер (1707-1783) родился в Базеле, в семье пастора. В 16 лет стал магистром. Проявлял выдающиеся способности. В школе ему было делать нечего, бегал на лекции в университет. С ним занимался персонально Иоганн Бернулли. Занимался медициной, физиологией, кораблестроением, физикой, математикой, когда ему было порядка 17-18 лет. В 18 послал труд о расположении мачты на корабле в Парижскую академию наук, хотел на кафедру физики. Его не взяли из-за возраста - 18 лет. Пришел только положительный отзыв. В 1727 году его пригласили в Россию братья Бернулли, и он приехал на кафедру физиологии в тот день, когда скончалась Екатерина I. Прекратилось субсидирование академии наук, отношение к преподавателям испортилось. Эйлер подумывал о возвращении в Европу моряком во флот. Но к счастью, один из профессоров-физиков уехал, и его место занял Эйлер. Потом он занял кафедру математики в 23 года. Он прожил в России с 1727 по 1741 и с 1766 по 1783 до своей смерти. Каждую математическую проблему получал из практической задачи. Лаплас: "Читайте Эйлера, учителя всех нас" (с).

В 1736 лишился зрения на один глаз от невероятного утомления. Было много русских учеников. Переписывался с Ломоносовым, когда уехал в Германию. После кончины Анны, при регенстве, дела стали совсем плохо и он уехал в Берлин. Возглавил в Академии наук кафедру математики. Но с русскими отношения не порвал, все отправлял в Россию.

В 1766 возвращается в Петербург, здоровье ухудшилось и он потерял зрение на второй глаз. Но все равно сотнями публиковал статьи. Он диктовал статьи сыну, тоже будущему академику Эйлеру. После смерти Эйлера было академиков десятка полтора, которые дорабатывали идеи Эйлера, которыми тот фонтанировал.

За свою жизнь опубликовал 889 работ. Тогда соавторства не было. +3000 писем математического содержания. Математика, механика, астрономия, медицина, морское дело, баллистика, артиллерия, финансовое дело, музыка, горное дело, теория музыки, картография, страховое дело. Причем вторую статью с похожим содержанием он не делал. При жизни – порядка 40 томов его изданий. 72 тома издано, и то это еще не до конца. Умер Эйлер - на долгое время математика в России заглохла. Эйлера ругают, что у того много неточностей. Но ведь он почти никогда не ошибался.

Условие Коши-Римана - это Эйлер и Даламбер.

Ряды Фурье - это Эйлер.

Ввёл понятие двойного интеграла.

Альфа-бета-гамма функции тоже.

Самый базовый его труд - дифференциальное исчисление. Создал теорию ОДУ, основы ДУЧП. Диффур с постоянными коэффициентами чаще всего решаются через подстановки Эйлера. Он пишет книгу и включает в неё все известные способы решения диффуров, в т.ч. и им самим изобретёнными. О единственности он не задумывался. Не разделял уже действительные и комплексные аргументы - в общем случае делал.

Начал классифицировать кривые по степени.

В России много занимался картографией. Надо было получить карту России. В 1735 совестно с Гензиусом привел картографию России в адекватное состояние, не хуже даже Германии.

Эйлер дал глобальную идею уравнений с параметрами.

Занимался судовождением: определением местоположения в океане.

Астрономией: издал работу по движению Луны, получил за нее премию. Создавал приборы для изучения звезд (у Ньютона были телескопы, но большие), разработал маленькие телескопы.

Решал артиллерийские задачи (как запустить снаряд, чтобы подальше улетел) – этим уже Бернулли занимался, но не все довел до конца и сделал ошибки.

Есть куча формул Эйлера, методов Эйлера, подстановки, уравнение, характеристики, углы, интегралы, функции, числа. Например, число lim(1 + ½ + … + 1/n - ln(n)) = 0,577… или соотношение для планарных графов: n + p – q = 2.

Много работ из разных повседневных областей: качество пожарного насоса, как оценить квалификацию машинных дел подмастерья.

Чарльз Бэббидж родился 26 декабря 1791 года в Лондоне. Его отец, Бенджамин Бэббидж, был банкиром. Мать звали Элизабет Бэббидж. Её девичья фамилия Тип (Teape). В детстве у Чарльза было очень слабое здоровье. В 8 лет, его отправили в частную школу в Альфингтоне на воспитание священнику. На тот момент его отец уже был достаточно обеспечен, чтобы позволить обучение Чарльза в частной школе. Бенджамин Бэббидж попросил священника не давать Чарльзу сильных учебных нагрузок из-за слабого здоровья.

После школы в Альфингтоне Чарльз был отправлен в академию в Энфилде, где по существу и началось его настоящее обучение. Именно там Бэббидж начал проявлять интерес к математике, чему поспособствовала большая библиотека в академии. После обучения в академии, Бэббидж обучался у двух репетиторов. Первый был священником, жившим возле Кембриджа. По словам Чарльза, священник не дал бы ему тех знаний, который он мог получить, обучаясь у более опытного репетитора. После священника у Бэббиджа был репетитор из Оксфорда. Он смог дать Бэббиджу основные классические знания, достаточные для поступления в колледж.

В 1810 году Бэббидж поступил в Тринити-колледж в Кембридже. Однако, основам математики он обучался самостоятельно по книжкам. Он тщательно изучал труды Ньютона, Лейбница, Лагранжа, Лакруа, Эйлера и других математиков академий Санкт-Петербурга, Берлина и Парижа. Бэббидж очень быстро обогнал своих преподавателей по знаниям и был сильно разочарован уровнем преподавания математики в Кембридже. Более того он заметил, что Британия в целом заметно отстала от континентальных стран по уровню математической подготовки.

В связи с этим, он решил создать общество, целью которого являлось внесение современной европейской математики в Кембриджский университет. В 1812 году Чарльз Бэббидж, его друзья, Джон Гершель (John Herschel) и Джордж Пикок (George Peacock) и ещё несколько молодых математиков основали «Аналитическое общество». В 1816 году они опубликовали переведённый ими на английский язык «Трактат по дифференциальному и интегральному исчислению» французского математика Лакруа, а в 1820 году опубликовали два тома примеров, дополняющих этот трактат. Аналитическое общество своей активностью инициировало реформу математического образования вначале в Кембридже, а затем и в других университетах Британии.

В 1812 году Бэббидж перешёл в колледж Св. Петра. А в 1814 году он получил степень бакалавра. В том же году Чарльз Бэббидж женился на Джорджии Витмур, и в 1815 году они переехали из Кембриджа в Лондон. За тринадцать лет брака у них было восемь детей, но пятеро из них умерли в детстве. В 1816 году он стал членом Королевского Общества Лондона. К тому времени он написал несколько больших научных статей в разных математических дисциплинах. В 1820 году он стал членом Королевского Общества Эдинбурга и Королевского Астрономического Общества. В 1827 году он похоронил отца, жену и двоих детей. В 1827 году он стал профессором математических наук в Кембридже, и занимал этот пост в течении 12 лет. После того, как он покинул этот пост, он большую часть своего времени посвятил делу его жизни - разработке вычислительных машин. Последние годы жизни Бэббидж посвятил философии и политической экономии. Чарльз Бэббидж умер в возрасте 79 лет 18 октября 1871 года.

Малая разностная машина

Впервые Бэббидж задумался о создании механизма, который позволил бы производить автоматически сложные вычисления с большой точностью в 1812 году. На эти мысли его натолкнуло изучение логарифмических таблиц, при пересчёте которых были выявлены многочисленные ошибки в вычислениях, обусловленные человеческим фактором. Ещё тогда он начал осмысливать возможность проведения сложных математических расчётов при помощи механических аппаратов.

Также очень большое влияние на Бэббиджа оказали работы французского учёного барона де Прони, который предложил идею разделения труда при вычислении больших таблиц (логарифмических, тригонометрических и др.). Он предлагал разделить процесс вычисления на три уровня. Первый уровень — несколько выдающихся математиков, подготавливающих математическое обеспечение. Второй уровень — образованные технологи, которые организовывали рутинный процесс вычислительных работ. А третий уровень занимали сами вычислители, от которых требовалось лишь умение складывать и вычитать. Идеи Прони навели Бэббиджа на мысль о замене третьего уровня (вычислителей) механическим устройством.

Однако, Бэббидж не сразу начал заниматься развитием идеи построения вычислительного механизма. Лишь в 1819 году, когда он заинтересовался астрономией, он более точно определил свои идеи и сформулировал принципы вычисления таблиц разностным методом при помощи машины, которую он впоследствии назвал разностной. Эта машина должна была производить комплекс вычислений, используя только операцию сложения.

Несмотря на неудачу с разностной машиной, Бэббидж в 1834 году задумался о создании программируемой вычислительной машины, которую он назвал аналитической (прообраз современного компьютера). В отличие от разностной машины, аналитическая машина позволяла решать более широкий ряд задач. Именно эта машина стала делом его жизни и принесла посмертную славу. Он предполагал, что построение новой машины потребует меньше время и средств, чем доработка разностной машины, так как она должна была состоять из более простых механических элементов. С 1834 года Бэббидж начал проектировать аналитическую машину.

Архитектура современного компьютера во многом схожа с архитектурой аналитической машины. В аналитической машине Бэббидж предусмотрел следующие части: склад, фабрика или мельница, управляющий элемент и устройства ввода/вывода информации.

Склад предназначался для хранения как значений переменных, с которыми производятся операции, так и результатов операций. В современной терминологии это называется памятью.

Мельница (арифметико-логическое устройство, часть современного процессора) должна была производить операции над переменными, а так же хранить в регистрах значение переменных, с которыми в данный момент осуществляет операцию.

Третье устройство, которому Бэббидж не дал названия, осуществляло управление последовательностью операций, помещение переменных в склад и извлечение их из склада, а также выводом результатов. Оно считывало последовательность операций и переменные с перфокарт. Перфокарты были двух видов: операционные карты и карты переменных. Из операционных карт можно было составить библиотеку функций. Кроме того, по замыслу Бэббиджа, Аналитическая машина должна была содержать устройство печати и устройство вывода результатов на перфокарты для последующего использования.

Для создания компьютера в современном понимании оставалось лишь придумать схему с хранимой программой, что было сделано 100 лет спустя Эккертом, Мочли и Фон Нейманом.

Бэббидж разрабатывал конструкцию аналитической машины в одиночку. Он часто посещал промышленные выставки, где были представлены различные новинки науки и техники. Именно там состоялось его знакомство с Адой Августой Лавлейс (дочерью Джорджа Байрона), которая стала его очень близким другом, помощником и единственным единомышленником. В 1840 году Бэббидж ездил по приглашению итальянских математиков в Турин, где читал лекции о своей машине. Луиджи Менабреа, преподаватель туринской артиллерийской академии, создал и опубликовал конспект лекций на французском языке. Позже Ада Лавлейс перевела эти лекции на английский язык, дополнив их комментариями по объёму превосходящих исходный текст. В числе прочего она составила план операций для аналитической машины, с помощью которых можно решить уравнение Бернулли, которое выражает закон сохранения энергии движущейся жидкости. Именно поэтому Аду Лавлейс справедливо называют первым программистом. Однако аналитическая машина так и не была закончена. Вот, что писал Бэббидж в 1851 году: «Все разработки, связанные с Аналитической машиной, выполнены за мой счёт. Я провёл целый ряд экспериментов и дошёл до черты, за которой моих возможностей не хватает. В связи с этим я вынужден отказаться от дальнейшей работы». Несмотря на то, что Бэббидж подробно описал конструкцию аналитической машины и принципы её работы, она так и не была построена при его жизни. Причин этому было много. Но основными стали: полное отсутствие финансирования проекта по созданию аналитической машины и низкий уровень технологий того времени. Бэббидж не стал в этот раз просить помощи у правительства, так как понимал, что после неудачи с разностной машиной ему всё равно откажут.

Для денег для создания аналитической машины Бэббидж разработал беспроигрышную систему ставок на скачках. В итоге они проигрались и Лавлайс пришлось закладывать фамильные драгоценности. Бэббидж даже писал роман для получения денег на построение аналитической машины.

Только после смерти Чарльза Бэббиджа его сын, Генри Бэббидж, продолжил начатое отцом дело. В 1888 году Генри сумел построит по чертежам отца центральный узел аналитической машины. А в 1906 году Генри совместно с фирмой Монро построил действующую модель аналитической машины, включающая арифметическое устройство и устройство для печатания результатов. Машина Бэббиджа оказалась работоспособной, но Чарльз не дожил до этих дней.

В 1864 году Чарльз Бэббидж написал: «Пройдёт, вероятно, полстолетия, прежде чем люди убедятся, что без тех средств, которые я оставляю после себя, нельзя будет обойтись». В своём предположении он ошибся на 30 лет. Только через 80 лет после этого высказывания была построена машина МАРК-I, которую назвали «осуществлённой мечтой Бэббиджа». Архитектура МАРК-I была очень схожа с архитектурой аналитической машины. Говард Айкен на самом деле серьёзно изучал публикации Бэббиджа и Ады Лавлейс перед созданием своей машины. Причём, его машина идеологически незначительно ушла вперёд по сравнению с недостроенной аналитической машиной. Производитльность МАРК-I оказалось всего в десять раз выше, чем расчётная скорость работы аналитической машины.

В материалах Бэббиджа и комментариях Лавлейс намечены такие понятия, как подпрограмма и библиотека подпрограмм, модификация команд и индексный регистр, которые стали употребляться только в 50-х годах XX века. Сам термин «библиотека» был введён Бэббиджем, а термины «рабочая ячейка» и «цикл» предложила Ада Лавлейс. Её работы в этой области были опубликованы в 1843 году. Однако в то время считалось неприличным для женщины издавать свои сочинения под полным именем и,Лавлейс поставила на титуле только свои инициалы. Поэтому её математические труды, как и работы многих других женщин-учёных, долго пребывали в забвении. Умерла она в раннем возрасте от неудачных родов.

К середине XIX века петербургскими математиками были получены значительные результаты. В первой половине столетия математическая деятельность концентрировалась вокруг М.В.Остроградского, В.Я.Буняковского и их учеников, которые тяготели к математической физике.

Михаил Васильевич Остроградский (1801 - 1861) родился на Украине в помещичьей семье. Учился в гимназии для бедных, учился очень неважно. Хотел быть гвардейским офицером, всю жизнь мечтал о военной карьере. Но его отговорили и он поступил, нехотя, в университет Харькова. Полтора года проучился ни шатко, ни валко. Потом поселился в квартире у одного математика, и тот заинтересовал его математическими проблемами. И он до конца второго года прошел полный курс университета. Фантастически сдал экзамен. Ректор университета предложил его не только дипломировать, но и присвоить степень кандидата наук. Однако ему не дали даже диплома за отказ посещать лекции по богословию. Остроградский обиделся и уехал в Париж получать образование, в период 1822 - 1828 годов. Он слушал лекции многих видных ученых Франции: Фурье, Пуассона, Коши, Лапласа и др. Знакомство с их работами определило научные интересы Остроградского - математическая физика и вообще проблемы естествознания. Быстро написал работу по вычислениям интегралов, она привлекла внимание Коши. В 1825 году писал о движении жидкости на поверхности цилиндра. Еще раз заслужил одобрение Коши.

Когда Остроградский вернулся в Россию, он уже был известен в научных кругах. В 1830 году он избирается в Академию наук (не имея диплома о высшем образовании). Он разрабатывает математические вопросы в различных областях естествознания: теории тепла, распространении волн, колебании упругих сред, теории неупругого удара. Значительными достижениями были обобщение вариационного принципа наименьшего действия Гамильтона для материальных систем (принцип Остроградского - Гамильтона), а также установление необходимых условий экстремума функционала для функций многих переменных (уравнения Эйлера - Остроградского).

В связи с задачами математической физики Остроградский получил фундаментальные результаты в математическом анализе. Это, прежде всего, формула преобразования интеграла по объему в интеграл по поверхности,

, формула Гаусса - Остроградского. В интегральном исчислении широко используется правило Остроградского интегрирования правильных рациональных дробей P(x)/Q(x). Остроградский ввел в математику правило замены переменных в кратных интегралах.

Дал строгое решение задачи о распространении тепла в жидкости. 1834 – статья о вычислении вариации кратных интегралов. Переход от n-кратных к (n-1)-кратных интегралам. В Европе этот результат не был известен, его потом переоткрыли с ошибками и автор получил премию. В 1835 году внес улучшения в метод Ньютона. Теория страхования, азартных игр, статистического контроля качества продукции. Применял теорию вероятностей к судебным делам, из-за чего вызвал волну скептицизма по отношению к этой отрасли науки.

Соратник Остроградского Виктор Яковлевич Буняковский (1804 - 1889) также получил образование в Париже, где он жил с 1820 по 1825 год. Получив в Париже степень доктора, он вернулся в Петербург и стал работать в университете. В 1830 он избирается академиком, а с 1864 года до своей смерти является вице - президентом Академии наук. Буняковский - автор многочисленных работ по математическому анализу, теории чисел, теории вроятностей. Он создал первый русский учебник “ Основания математической теории вероятностей” , изданной в 1846 году. Ему принадлежит известное в анализе неравенство Буняковского для интегралов

[.

Проблема демографии, народонаселения. Его называют первым демографом.

Новую петербургскую математическую школу еще при жизни Острогадского возглавил Пафнутий Львович Чебышев (1821-1894). Он родился в Калужской губернии в семье дворянина. Хорошее математическое образование получил в Московском университете, где учился у профессора Н.Д. Брашмана, человека передовых взглядов. Еще будучи студентом, Чебышёв получил серебряную медаль за вычисление корней уравнений, после защитил диссертацию по теории вероятностей. Потом поехал работать в петербургский университет. Наиболее яркий представитель петербургской школы, после защиты докторской диссертации избирается профессором. Все его работы навеяны сугубо прикладными задачами.

Результаты по теории простых чисел, полученные в диссертации и в ряде статей этого периода, выдвинули Чебышева в число ведущих математиков Европы. Здесь он впервые получил строгие результаты по асимптотическому распределению простых чисел: функция , обозначающая число простых чисел, меньших x, при ведет себя, как /. Чебышёв аналитическим путем показал, что a*x/ln x < p(x) < b* x/ ln x, а = 0,921, b = 1,06. Тогда существовала гипотеза Бертрана о том, что между двумя какими-то числами (н и 2н) есть простое число. Чебышёв получил эту гипотезу между делом простым и элементарным способом.

Чебышеву принадлежат фундаментальные результаты по теории вероятностей и ее обоснованию. Он разработал метод моментов и доказал предельную теорему для сумм независимых случайных величин, из которой как частные случаи следуют теоремы Бернулли и Пуассона. Используя подход Чебышева его выдающийся ученик А.А. Марков существенно расширил условия выполнения закона больших чисел и получил теорему, из которой при условии независимости случайных величин следуют результаты Чебышева. Другой выдающийся ученик Чебышева А.М.Ляпунов систематически использовал метод характеристических функций и доказал предельную теорему для условий менее ограничительных, чем Марков. Кроме того, он оценил погрешности, возникающие от замены закона распределения суммы нормальным законом. А.А.Маркову также принадлежит разработка теории так называемых цепей Маркова. Благодаря работам Чебышева, Маркова и Ляпунова теория вероятностей приобрела вид строгой математической теории. Асимптотические разложения функций распределения.

В анализе он доказал теорему об условиях интегрируемости дифференциального бинома: интеграл , где m, n, p - рациональные, выражается через элементарные функции , если одно из чисел p, является целым.

Он создал теорию наилучшего равномерного приближения функций и сформулировал теорему о необходимых и достаточных условиях наилучшего приближения непрерывной функции многочленом. Прежде всего, поговорим о многочленах Чебышёва, приближающих функцию, непрерывную на [a,b]. Возьмем класс многочленов Pn(x). Рассмотрим максимальное уклонение полинома от функции. Поскольку это величина неотрицательная, то есть нижняя грань, следовательно, есть точная нижняя грань. Имеется в виду нижняя грань максимального уклонения среди всех многочленов n-ной степени. Грань называется наилучшим приближением функции. А сам многочлен, на котором она (грань) достигается, называется многочленом наилучшего приближения функции. Критерий многочлена наилучшего приближения: чтобы алгебраический многочлен Pm(·) был полиномом наилучшего равномерного приближения непрерывной функции f(·) необходимо и достаточно существования на [a, b] по крайней мере (m + 2) точек x₀ < x₁ < ... < x_m+1 таких, что f(x_i) − Pm(x_i) = α(−1)ⁱ||f − Pm||, i = 0, 1, . . . , (n + 1), причем α = 1 или α = −1 для всех i одновременно (точки альтернанса – чередуем знаки и равенство по модулю).

Теория интегрирования. Несколько квадратурных формул. Оценки: интеграл f(x)dx интеграл g(x)dx <= (b-a) интеграл f(x)g(x)dx. Интегрирование биномов (x^m(a+bx^n)^p) – доказал, что берется, если p – целое, или (m+1)/n - целое, или (m+1)/n + p – целое.

Многочлен Чебышёва первого рода Tn(x) характеризуется как многочлен степени n со старшим коэффициентом 2n - 1, который меньше всего отклоняется от нуля на интервале [ − 1,1] среди многочленов заданной степени. Впервые рассмотрены самим Чебышёвым.

Также могут быть определены с помощью равенства Tn(z) = cos(narccosz).

Несколько многочленов Чебышёва первого рода

Марковых было два – отец и сын. Алгоритм Маркова – это сын.

Александр Михайлович Ляпунов занимался теорией дифференциальных уравнений, гидромеханикой, теорией вероятностей. Основные результаты - в теории устойчивости и движения механической системы с конечным числом параметров.

Ляпунов – другой ученик Чебышёва. Написал о нем статью с высочайшей оценкой его результатов. Родился в Ярославле в семье директора обсерватории, потом лицея. Ляпунов блестяще учился по всем предметам. Работал много, устанавливал себе жесткий режим. Для него ничего не существовало кроме работы. В 1876 Ляпунов оканчивает гимназию с золотой медалью и поступает в Санкт-Петербургский университет (сначала на факультет естественных наук, затем переходит на математический). Кабинетный ученый. Ответственно относился к научным работам, преподавательской деятельности. Защитил магистерскую диссертацию (вращение жидкости и фигуры равновесия, возникающие при этом) и перешел в Харьковский университет, там возглавляет кафедру механики и читает лекции. Скрупулезно готовился к своим лекциям, студенты понимали, что он глубокий и интересный ученый. Ему боялись задавать вопросы. Поэтому выбирали одного студента, которому давали список вопросов, и он один задавал, так как один не боялся. Это был Стеклов, потом тоже стал известным.

Ляпунов публиковал свои работы только тогда, когда был убежден в новизне и полной безошибочности своих исследований. Пуанкаре предоставлял результаты, которые были лишь частями работы Ляпунова, причем с ошибками и получал за это степени и награды. А Ляпунов не счел это даже достаточным для диссертации. Считал, что нельзя ограничиваться интуицией и плохими приближениями. Его результаты выдерживают любую критику.

Ляпунов изучал равновесие фигур вращающейся жидкости (1905 - книга о фигурах равновесия). Образование планет, планетные системы – образование из частиц притягивающейся жидкости. К тому моменту было известно, что эллипсоид – фигура равновесия. Но что если придать ускорение? Что если материал неоднородный? Это задачи очень сложной математики. Получил ряд полезных результатов. Сфера - тоже фигура равновесия. Устойчивость равновесия. Изменения однородностей жидкостей. Получал системы, уравнения, рассматривал их детальней, чем было до сих пор. Навел полный порядок в этом деле. Вот Пуанкаре действовал интуитивно, и на его результатах астроном Дарвин построил теорию, которую Ляпунов разнес в пух и прах. В конце жизни Ляпунов возвращался к этой проблеме. По существу закрыл ее.

Устойчивость по Ляпунову стала классикой. Ни одна ракета без этого не полетит. Занимался уравнениями в частных производных. Зависимость потенциала от зарядов на поверхности. Поверхности Ляпунова. Связано с задачей Дирихле для уравнения Лапласа. Теория вероятностей. Хотел превзойти результаты Маркова по ЦПТ. Но пользовался другим методом - тот использовал метод моментов, а Ляпунов рассматривал близкие к случайным величинам величины. Метод характеристических функций. У них была «творческая борьба». Вдвоем довели до ума теорему. Устойчивость механических систем. Исследование предельного поведения стремящейся к бесконечности случайной переменной.

Ляпунов погиб в революцию. Жена заболевает туберкулезом. Он узнает, что революционеры сожгли его библиотеку. В день смерти жены застрелился.

Софья Васильевна Ковалевская (1850-1891) занималась астрономией, функциональным анализом, теорией потенциала, математической физикой. Она известна также и своими литературными произведениями (напр., "Нигилистка"), писала стихи, поэмы, общалась с Достоевским. Ее спрашивали, математик она или поэт.

Родилась в небедной семье, ее отец возглавлял арсенал, был генералом. В 8 лет переехала в загородное имение. Много читала, хотя и беспорядочно, была любознательна. Бытует легенда, что ее комнату обклеили страницами матана Остроградского, тк обоев не хватило, и впоследствии ей было легче в университетах.

Отец возражал против занятий девочки математикой, но ее дядя настоял на том, что у нее хорошее мышление. С ней занимался Остролюбский. Об обучении в университете речи быть не могло, это было запрещено. Она фиктивно вышла за палеонтолога Ковалевского в 18 и уехала в Германию. В Европе ее сестру посадили в тюрьму во Франции. Ковалевские организовывали побег. Поначалу ее не пускали на лекции в Германии. Пришлось приехать Ковалевскому, давить авторитетом, чтобы ее допустили до занятий. Но в университете было слишком просто для нее и она поехала к Вейерштрассу в Берлин. В университет ее опять не пустили, она приехала к нему в квартиру. А тот считал, что женщина должна дома сидеть. И дал ей три хороших задачи. Она решила сразу. Пришлось с ней работать.

За три года работы с Вейерштрассом Ковалевская получила фундаментальный результат о существовании и единственности аналитического решения задачи Коши для дифференциального уравнения в частных производных. Он известен в математике как теорема Коши - Ковалевской. В это же время она опубликовала результаты исследований по форме колец Сатурна (показала, что имеют яйцевидную форму) и по эллиптическим интегралам (привела к ним абелевы). За эти работы Геттингенский университет по представлению Вейерштрасса присудил ей без защиты степень доктора философии.

В Европе она была знаменитым математиком. Но в России ей максимум разрешали заниматься математикой с девочками 8-10 лет. Ей это не нравилось, но она хотела жить в России. Ковалевские пустились в спекуляции по недвижимости. Помогала женщинам фиктивно выходить замуж, чтобы уехать заграницу получать образование. Ее старался вернуть в Европу Вейерштрасс. Писал ей письма, отправил к ней на уговоры ле Флёра (из-за которого математики лишены Нобелевской премии), но даже его чары не повлияли на нее. Она порвала с математиками. После Ковалевский покончил жизнь самоубийством, тк переиграл на спекуляциях. Для Софьи это было тяжело (брак уже не был фиктивным), но у нее не вышло тоже застрелиться. Тут она поняла, что в России делать больше нечего, и уехала в Стокгольм. Стала там доцентом, профессором.

Опубликовала работу по преломлению света через кристалл (двойное преломление). Читала курсы лекций по математике. За 8 лет, до своей кончины, она подготовила и прочла 12 курсов, включая курс механики. Пользовалась феноменальным успехом у студентов. Ее заинтересовала задача, которую Берлинская академия наук выставляла на конкурсы: впервые после Эйлера и Лагранжа получила новые результаты в решении задачи о вращении твердого тела вокруг неподвижной точки. Очень многие брались за задачу, никто не мог решить. И тут побеждает анонимная блестящая работа. Математический мир и так был потрясен, а тут выяснилось, что это женщина. Ее результаты были удостоены премий Парижской и Шведской академий наук (открытие третьего классического случая разрешимости задачи о вращении твердого тела). Через несколько лет решение этой проблемы удалось существенно продвинуть Ляпунову.

В 1891 году заболела туберкулезом и скончалась.

Еще при Евклиде было установлено, что не все есть число. Кризис при появлении иррациональных чисел.

Кризис комплексных чисел.

Задачи обоснования математики. Теоретико-множественные представления. Требовалось навести порядок (18-19 век). Кризис при теории множеств. Множество всех подмножеств множества А не равномощно ни множеству А, ни его подмножествам - появляются противоречия.

Были попытки объяснить мир при помощи логики, один из основоположников – Рассел. Но сам Рассел нашел противоречия и в логике, и в теории множеств Кантона. Обнаружились антиномии, выявленные с помощью чистой логики. Сельский брадобрей бреет только тех, кто сам себя не бреет. То, что я говорю – ложь. Их каждого правила есть исключения. Таким образом, получается куча парадоксов. Гётель в 1931 доказывает, что нельзя доказать непротиворечивость ни одной полной аксиоматической системы. Сводить математику к логике не вышло. Хотя вообще с логикой любопытно – есть мнение, что логику нельзя победить потому, что ее можно победить только с помощью логики.

Дорр Фельт разработал арифмометры в 1886.

Ванневар Буш в 1930-х разработал дифференциальные решатели для уравнений dz = y dx, позже появились электрические версии.

Далее появились первые электронные компьютеры. Конрад Цузе – создатель Z1 (1936), механического калькулятора, включавшего управляющую систему и память. Атанасов и Берри создали первый электрический цифровой компьютер в 1939. Использовали электронные лампы для сохранения информации, также впервые использовали двоичную систему. Далее появились ENIAC (1944) и UNIVAC (1951). Второй был первым полностью электронно-цифровым компьютером в США. Электронные лампы господствовали 1941 – 1954, это было первое поколение.

Грейс Хоппер нашёл мотылька в реле, которое сбоило. Назвал это “debugging” компьютера, т.е. термин восходит к слову «насекомое».

В 1948 - первый транзистор, но второе поколение, его использующее, появилось в 1955. Третье поколение с интегральными схемами и ОС – 1965-1980. Первый микропроцессор – 1971. Рождение ПК – 1975.

Алан Тьюринг (1912 – 1954):

Тезис Чёрча-Тьюринга. Любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга

Криптография. Тьюринг помогал взломать код Энигмы. Построен первый программируемый компьютер Колоссус, который базировался на концепции универсальной машины, потенциальной скорости и надёжности электронных технологий, неэффективности разностных машин для различных логических процессов. Шифр-код был расшифрован в 1943. После все компьютеры были разрушены по приказу Черчилля

Основатель направления ИИ. Тест Тьюринга опубликован в 1950 году. Человек обменивается сообщениями на естественном языке с двумя собеседниками (человек и компьютер). Если человек не может определить кто есть кто, то считается что компьютер прошёл тест. Переписка должна производиться через контролируемые промежутки времнени. Тьюринг оценил, что программы в 2000 году пройдут тест, но пока не подошли даже близко

МТ. Проблема самоприменимости МТ. Универсальная МТ

фон Нейман

Из-за разногласий в команде разработчиков реализация проекта фон Неймана в США затянулась. Принципы фон Неймана схожи с принципами аналитической машины Бэббиджа, фактически с нее списаны. Как минимум он точно знакомился с его работами. Работы в квантовой физике, функциональном анализе, теории множеств. Создатель теории игр и теории клеточных автоматов.

Первая ЭВМ с хранимой программой EDSAC (Electronic Delay Storage Automatic Calculator) была построена в Англии в 1949 г. под руководством Мориса Уилкса. Английские ученые опирались на собственный опыт разработки электронных вычислительных устройств во время Второй мировой войны.

Конрад Цузе (1910 – 1995) сконструировал первые компьютеры Z1, Z2, Z3, Z4 и придумал язык Планкалкюль.

Принципы Цузе

• Двоичная система счисления;

• Использование устройств, работающих по принципу “да/нет” (логические 1 и 0);

• Полностью автоматизированный процесс работы вычислителя;

• Программное управление процессом вычислений;

• Поддержка арифметики с плавающей запятой;

• Использование памяти большой емкости.

Первая попытка создать высоко-уровневый язык программирования принадлежит гениальному Конраду Цузе (конец 1940-х годов), разработавшему Plancalcul (планировщик вычислений). «Plancalcul родился исключительно как результат теоретической работы, без всякой связи с тем, появится или нет в обозримом будущем машины, подходящие к программам на Plancalcul».

Эдсгер Вайб Дейкстра (1930 – 2002)

• Математическая логика

• Algol-60

• Концепция семафоров

• Алгоритм Дейкстры (про поиск пути)

• Борьба с оператором GOTO

• Студентов, ранее изучавших Бейсик, практически невозможно обучить хорошему программированию. Как потенциальные программисты они подверглись необратимой умственной деградации

• Вопрос «умеет ли компьютер думать» имеет не больше смысла, чем вопрос «умеет ли подводная лодка плавать»

• Проекты, предлагающие программирование на естественном языке, гибельны по своей сути

• Дейкстра назвал модель IBM/360 (прообраз советской ЕС ЭВМ) величайшей диверсией Запада против СССР

• На пустом диске можно искать вечно

• Если отладка — процесс удаления ошибок, то программирование должно быть процессом их внесения

Fortran = FORmula TRANslator. Первый высокоуровневый язык программирования Fortran был разработан в фирме IBM под руководством Джона Бэкуса (Backus, John; р. 1924).

Работа над языком началась в 1954 г., первая реализация для IBM 704 в выполнена в 1957 г.

BASIC = Beginners All-purpuse Symbolic Instruction Code. Язык Basic был разработан в 1964 г. в Дармутском колледже в г. Хановере Авторы языка Basic - Джон Кемени (1926-1993), Томас Курц (р. 1928). Будущие создатели Microsoft Пол Аллен (р. 1954) и Билл Гейтс (р. 1955) познакомились с Бэйсиком, работая в компьютерном классе школы в Сиэтле.

COBOL = COmmon Business-Oriented Language. Разработчики языка Cobol получили шуточный обелиск, присланный в их адрес в качестве намека на безнадежно медленную работу, способную похоронить саму идею. Считается языком для бухгалтеров. Грейс Хоппер.

Основные свойства языка Cobol:

• независимость программ от оборудования;

• независимость программ от данных;

• сложные структуры данных;

• синтаксис, приближенныйк естественному английскому языку.

ALGOL = ALGOritmic Language. В 1958 году в Цюрихе (Швейцария) состоялась международная конференция, предложившая проект нового универсального международного языка программирования Algol-58. В 1960 году на парижской конференции была принята окончательная версия под названием Algol-60. Синтаксис Алгола-60 сформировал стандарт для всех последующих языков программирования

• машинная независимость;

• формальный синтаксис;

• описание переменных и блочная структура;

• рекурсия

Нормальная форма Бэкуса-Наура (БНФ)

<цифра>::= 1|2|3|4|5|6|7|8|9|0

<целое без знака>::= <цифра>| <цифра> <целое без знака>

Член комитета по Алголу-68 Никлаус Вирт (Wirth, Niklaus; р. 1934) был против принятия переусложненного стандарта.

В знак доказательства своей правоты он разработал в 1971 г. простой и ясный алголоподобный язык, предназначенный прежде всего для обучения студентов в Федеральном техническом университете в Швейцарии. В честь изобретателя первой вычислительной машины Вирт назвал язык Паскалем. Новую жизнь языку Pascal дал Филипп Кан (р. 1938) – создатель компилятора Turbo Pascal для IBM PC и основатель компании Borland (1984 г.)

Simula = SIMULAlation За разрабртку языка Simula Кристен Нигорд (1926-2002) и Оле-Йохан Дал (1931-2002) были удостоены высшей награды компьютерного сообщества – медали Тьюринга.

Язык Си (С) был создан Деннисом Ричи (1941-2011) в 1973 году в Bell Labs в ходе разработки операционной системы UNIX. Он развивал язык Би (B), который основывался на созданном в Кембриджском университете языке BCPL (от Basic Combined Programming Language), который в свою очередь был потомком Алгола-60. Бьярн Страуструп (р. 1950) ввел в язык С объекты и превратил его в С++.

В 1995 г. фирма Sun Microsystems представила язык Java для программирования в интернете.

Он возник в ходе реализации проекта Oak («Дуб»), целью которого было создание системы программирования бытовых микропроцессорных устройств. Джеймс Гослинг – автор Java.

Lisp = LISt Processing Язык Lisp создан в 1960 году Джоном Маккарти (р. 1927 ) в Массачусетском технологи-ческом институте на теоретическом фундаменте лямбда-исчисления, предложенного еще в 1930 году известным американским логиком Алонзо Черчем.

Prolog = PROgramming for LOGic Теоретические основы языка были разработаны Робертом Ковальским в Эдинбургском университете (Шотландия) в конце 1960-х годов. Первая практическая реализация языка осуществлена Аленом Кольмари в Марсельском университете (Франция) в 1972 г.

Рефал = PЕкурсивных Функций АЛгоритмический Теоретические основы языка были разработаны Валентином Турчиным в МФТИ в конце 1966 году

Язык Logo, изобретен в 1967 г. в MIT выдающимся математиком и педагогом Сеймуром Пейпертом (р. 1928). Пейперт в 1958-1963 годах работал в Женеве у знаменитого психолога Жана Пиаже (Piaget, Jean), где занимался детьми и природой их мышления. Идейной основой Logo является язык Lisp

Основные парадигмы программирования:

• процедурное программирование (Fortran, Basic, Cobol, Algol, Pascal, Ada, С, Logo, FoxPro);

• объектно-ориентированное программирование (Simula, Smalltalk, Object Pascal, C++, Java, C#);

• визуально-событийное программирование (Visual Basic, Delphi, Visual C++, Visual Java, Visual FoxPro);

• функциональное программирование (Lisp, Рефал);

• логическое программирование (Prolog).